White Elephant is surprisingly effective
The holiday game of White Elephant gift exchange is beloved for obvious reasons: no pressure to find the perfect gift, socially-acceptable kleptomania, and juicy yet temporary drama.
But what if I told you it was also an amazingly-efficient way to distribute a bunch of gifts, so that everyone would like their gift? Playing White Elephant could save you hundreds of millions of hours next Christmas season.
Just look at the inputs: several gifts, and how each player values each of those gifts. What's the output? An assignment of gifts to people. If you squint at it, White Elephant is clearly an algorithm for resource allocation. But how effective is it?
How would you know if White Elephant is any good at getting people gifts that they actually like? I had no choice but to spend several days simulating games of White Elephant to check exactly how good it is.
Rules refresh
Everyone plays a slightly different variation of this game, so here is a refresher of the ruleset I'm using.
In a game of White Elephant, several people get together. Each person brings one gift, and each person will take home a (probably-different) gift.
- On the first turn, one person selects a gift and reveals it.
- On subsequent turns:
- A person selects and reveals a new gift, OR
- A person steals an already-revealed gift from a previous person.
- The person stolen-from must now select a new gift, or steal an opened one.
- The person stolen-from cannot immediately steal back the same gift.
- Each gift can only be stolen three times (not including the initial revealing).
- The game continues until all presents are revealed.
How do we know a game's outcome is "good"?
We also need to define some criteria for a "good" White Elephant outcome would be.
Each player has their own preferences for which gift(s) they prefer; in other words, the same gift can be (and usually is) valued differently by each player. Let's define that value as a number from 0 to 100, where 100 is the best possible gift. At the end of the game, each player will have a gift and corresponding 0-to-100 value.
There's lots of potential definitions of "good", as any philosopher would tell you. Would it be hubris to pass judgment on if a game's final outcome (assignment of gifts to players) is better than a different outcome? What about the risk of being chained to a rock for eternity, forced to decide whether the trolley hits your liver, or your two kidneys?
Anyways, I'm going to focus on three measures of goodness.
- Sum of happiness: the classical utilitarian way to do it. The group's happiness is equal to the sum of each player's happiness.
- Pareto-optimality: an outcome is Pareto-optimal if there is no outcome where every single person is happier. In other words, all other assignments would cause at least one person to be less happy, so there's no opportunity for "free lunch" improvement.
- Top-k choice: an outcome is good if enough people get one of their top-ranked choices. A person gets their top-1 choice if it's their favorite, top-2 if it's in their highest two preferences, and so on. For a given assignment, you can calculate how many players got their top-k choice for each k.
How do we know if White Elephant is "good" at producing good outcomes?
While sum of happiness and top-k choice can be calculated pretty easily (and Pareto optimality with a little more effort), looking at a single game's end result tells us nothing about how good White Elephant is across the universe of all possible assignments and preferences.
For example, let's take a 2-player game, where player 1 and player 2 both really want Gift A (value=100), and don't care about gift B (value=0). Regardless of who gets the gift, we end up with the following:
- Sum of happiness: 100 + 0 = 100.
- Pareto-optimal: True: you can't swap Gift A without making the former owner unhappy.
-
Top-k choice:
- Top-1: 1 player (whoever gets Gift A)
- Top-2: 2 players (for an N-player game, Top-N is always N)
So in this toy example, is 100 a good sum? It's arbitrary, since we know the other outcome is identical. Is a Top-1 of 1 good or bad? No, besides being similarly arbitrary, it's also entirely determined by the gift preferences. And we can only really say this with confidence because it's a comically small number of players.
For larger games, I really want to know, how good is it relative to other possible outcomes? If we looked across every permutation of assignments for a set of gift preferences, is a game of White Elephant better than average?
Methodology
In order to answer these questions, I wrote a White Elephant simulation in Python.
For a game with N players, there are N gifts. Each player has a different random set of preferences for those gifts, ranging from 0 to 100 (inclusive).
Following the rules above, on each player's turn, make a decision using generative AI the following
process:
- Examine the already-revealed gifts and find the highest-valued available gift. If that value is greater than or equal to 50, then steal it.
- If not, that means no currently-stealable gift is great. Reveal a new gift, hoping for the best.
Once the game ends, calculate the measures of goodness from above.
Sum of happiness and top-k choice are easy to compute from the final assignment. For Pareto optimality, we took the brute force option: for all possible permutations of gifts and players, check if any permutation is better for all players than the White Elephant outcome.
Since we already generated all permutations, we might as well calculate the sum of happiness for each. We can sort the resulting permutations by sum of happiness, and figure out where exactly our White Elephant outcome ends up.
Example game
For example, in a 4-player game, there are 4! = 24 possible outcomes for a given set of player preferences. Let's look at a specific set of preferences.
| Player | Gift A | Gift B | Gift C | Gift D |
| 1 | 49 | 97 | 53 | 5 |
| 2 | 33 | 65 | 62 | 51 |
| 3 | 100 | 38 | 61 | 45 |
| 4 | 74 | 27 | 64 | 17 |
In this table, the cells represent a player's value for that gift, e.g. Player 1 thinks Gift A is worth 49, Player 2 thinks that same Gift A is worth 33, and so on.
Simulating a White Elephant game from these starting conditions results in the following outcome:
| Player | Gift A | Gift B | Gift C | Gift D |
| 1 | 49 | 97 | 53 | 5 |
| 2 | 33 | 65 | 62 | 51 |
| 3 | 100 | 38 | 61 | 45 |
| 4 | 74 | 27 | 64 | 17 |
The total sum of happiness for this outcome is 97 + 51 + 61 + 74 = 283. The top-k results:
- Top-1: 2 (P1, P4 got their top picks)
- Top-2: 3 (P3 got their 2nd choice, and P1+P4 above did better)
- Top-3: 4 (P2 got their 3rd choice - all done)
Eyeballing it, that seems pretty good. But is there anything better?
Using the power of brute force, we can compare this against some other scenarios - it turns out, yes, there is a better outcome! There are also far worse outcomes...
| Player | Gift A | Gift B | Gift C | Gift D |
| 1 | 49 | 97 | 53 | 5 |
| 2 | 33 | 65 | 62 | 51 |
| 3 | 100 | 38 | 61 | 45 |
| 4 | 74 | 27 | 64 | 17 |
| Player | Gift A | Gift B | Gift C | Gift D |
| 1 | 49 | 97 | 53 | 5 |
| 2 | 33 | 65 | 62 | 51 |
| 3 | 100 | 38 | 61 | 45 |
| 4 | 74 | 27 | 64 | 17 |
The White Elephant outcome is 2nd-best out of all 24 possibilities. Note that even though the "best" outcome above has a higher total sum, it is not a Pareto improvement over the White Elephant outcome, since Player 4 loses 10 points of value by switching from Gift A to Gift C.
2 out of 24 is easy enough to understand in isolation, but it becomes messier when we consider games with a different number of players, because the worst possible rank changes based on the number of players (N!). We converted these to percentiles to make them easier to compare: White Elephant is equal or better than 23 of 24 outcomes, so it is 23 divided by 24 = ~95th percentile.
Finally, to consider the impact of the player's preferences, we ran multiple trials with random preferences. We simulated 10,000 different preference sets, for group sizes ranging from 2 (because it was trivial) and 9 (because that's the largest my laptop would do in a reasonable amount of time).
Predictions
Before we continue, take a guess: how good is White Elephant?
-
How often is the White Elephant result in the 99th percentile (top 1%) of potential outcomes, in terms of
sum of happiness?
- How about the 50th percentile (better than average)?
- How often is the White Elephant result Pareto-optimal?
-
In an N-player game, how many people get their favorite (top-1) choice?
- How about top-3?
I'll give you a hint: these answers vary based on N, the number of players. Knowing that, one final question: what changes in your predictions from N=2 to N=9?
Initial analysis
The following graphs show the rank-percentile distribution for 10,000 simulated games of White Elephant. Each bar represents 1% of the possible outcomes, where the right side is the best. Each game is a data point, and these are bucketed into percentiles - each bar represents 1% of the possible outcomes, where the left side is the best.
In this first graph for 5-player games, you can see that there are 120 possible outcomes for a starting set of preferences. Across 10,000 White Elephant games over different preference sets, about 14% (one in seven) of games ended up in the 99th percentile (top 1%) of possible outcomes!
Note: these graphs are hard to read on mobile, sorry - rotating your screen might help.You can click the arrows above to see how the distribution changes based on N. Go ahead, I'll wait.
...isn't that good, and a little surprising? I double-checked my code because it seemed too good to be true. (And I published some very ugly source code as well, so please let me know if there's something wrong!).
You can also see that the vast majority of outcomes are Pareto-optimal - a vanishingly small number for higher N. As the number of players grows, it appears to converge towards a stubborn 1% of non-optimal outcomes (though I have no idea why).
Top-k is really N different distributions, so it is shown here as a box-and-whiskers plot. The mean of each distribution is plotted as the black dotted line:
Is this good? Initially, I don't know how to interpret it - an average of 6.5 people getting their top-3 gift in a 9-player game seems pretty decent, but I don't really know what's possible. In hindsight now, to get better understanding, we might have to do some more math on the expected number of unique preferences, which depends on how preferences are generated.
Consider top-1. The best possible outcomes happen when everyone gets their top-1 gift. But it's possible for multiple people to want the same top-1, so overlapping preferences will reduce the best possible top-1. So what's the expected value of unique top preferences?
Since preferences are random, each person should have an equal chance of choosing any particular gift as
their favorite (...I think). This maps to the birthday problem: in a room with N people, what are the
odds that at least two people share a
birthday favorite gift? Wikipedia helpfully gives a closed-form solution for
number of days with at least one birthday, which lets us build the following table. (Extending the formula to top-k gifts is left as an exercise
for the reader.)
| Number of players | Unique gifts |
| 2 | 1.5 |
| 3 | 2.1 |
| 4 | 2.7 |
| 5 | 3.3 |
| 6 | 4 |
| 7 | 4.6 |
| 8 | 5.3 |
| 9 | 5.9 |
It seems like there is room for improvement at the top: White Elephant seems to sit at about 50% of ideal top-1 for any given N. I could check the data to see if it matches these predicted ideal top-1 values, but I am rapidly approaching my self-imposed deadline, so let's go to...
Intuition and room for improvement
While I thought it would be good, I didn't think it would be this good. But it makes sense!
Let's start with top-k. People should end up with a gift which is near the top of their preferences: this is baked into the algorithm directly, since players will steal the best-available gift.
Practically by definition, a good top-k is likely to have a good sum of happiness: more people are getting things they like, which corresponds to higher total scores.
Similarly, Pareto-optimality is very likely because players steal the best-available gift. If you see a non-optimal outcome, it implies that none of the players-who-should-swap were able to steal their preferred gift (because it hadn't been revealed yet, or because it had hit the max steal count already).
(Side note: top-1 = N, where every person gets their favorite gift, is equivalent to envy-freeness in fair division problems; it's very unlikely in White Elephant since each person must take exactly one gift.)
Now, satisfied with the goodness, I wanted to know more about the badness - what's going on in these long tails of poorly-performing White Elephant games?
I looked through the logs of a few poorly-performing games and noticed a pattern: these games occur when the first player (and sometimes, the next few) reveal a gift they don't like, and... they're just stuck with it. They never have the opportunity to steal because no one ever steals from them, and they just suffer as better gifts are revealed.
I realized I was missing a critical (and common) rule: the first player gets the opportunity to swap at the end of the game! This eliminates one common way to get "stuck", and also ensures that anyone stolen-from at the end gets to steal their favorite available gift with full knowledge of the possibilities (since all gifts are now revealed).
After hastily coding this rule and fixing the bugs, I ran my simulation for another 6 hours to see how it changed the results.
Adding the "last steal" rule
Take a look at the comparison: this noticeably shifts the distribution towards the right, regardless of the number of players. In the graph below, the original ruleset results are in red, while adding the "last steal" rule is shown in blue.
Pareto-optimality and top-k are also improved. With the "last steal" rule, Pareto optimality converges towards 0.5% of games being non-optimal: a 50% reduction. Top-k also shifts so that more people receive their top choices. You've had enough graphs by now, so I will spare you (read: I am making an excuse to avoid more graphing).
Nice. We've established that the "last steal" rule improves the outcomes of games, and this means you should adopt it in your own games, if you didn't use it already. If you need to justify it to someone, just send them this link.
So now we know White Elephant is an algorithm that produces pretty good results, with a lot less effort than brute force. How much less effort exactly?
Performance
For a brief estimate on performance, I used the built-in Python module cProfile to understand how much time was spent in different parts of the simulation program. See the resulting flamegraph (generated using SnakeViz) for a set of 5-player games below.
In the second row, (if you can read the tiny text), you can see that the brute force (purple) section took a bit longer than the White Elephant game itself (blue).
We could dive deeper to see which "hot" areas of code take the most time. For example, the gray subchunk of the White Elephant game is just computing the total score, which happens after each player's turn; we could probably improve the time by only calculating the score once at the end.
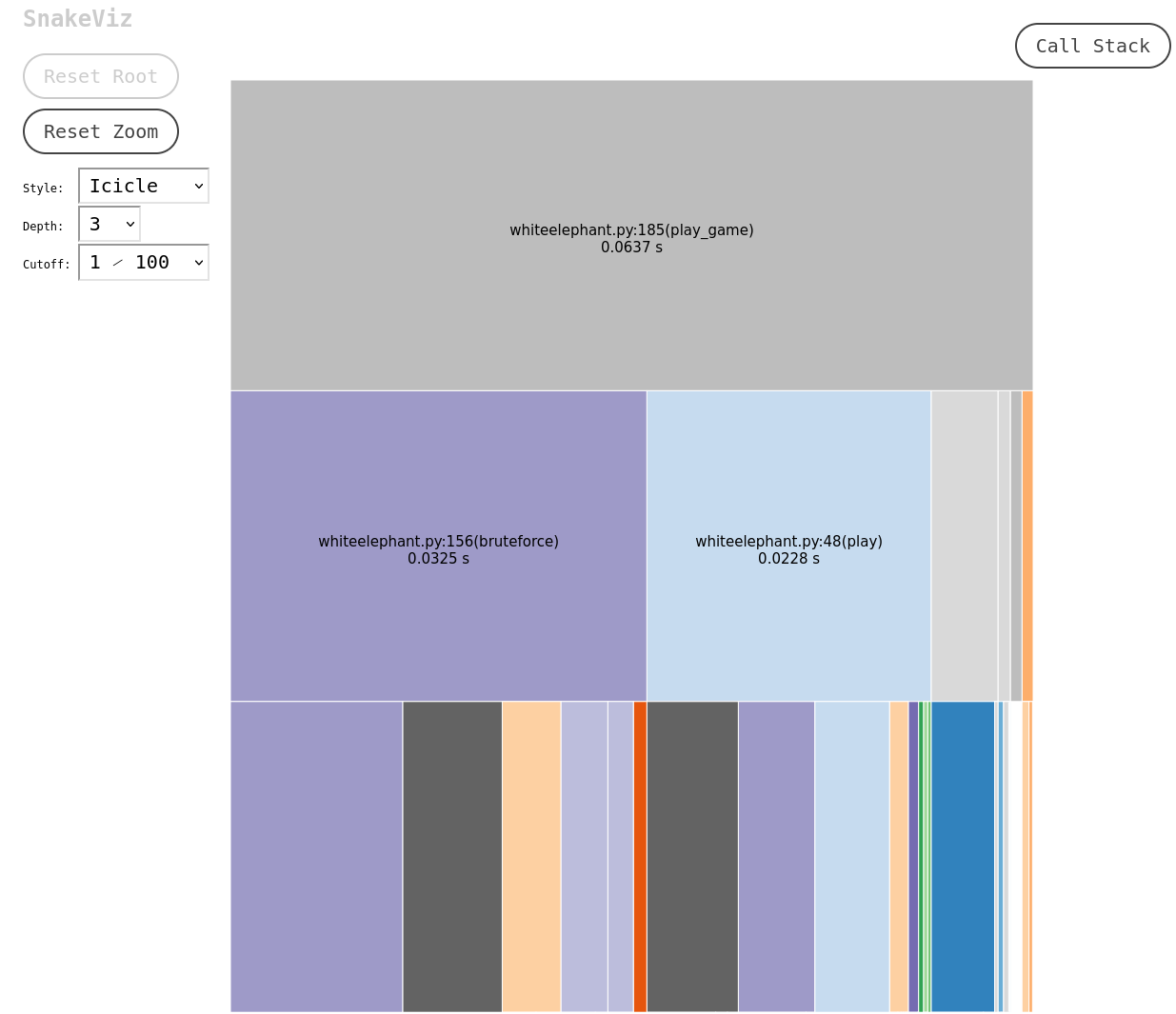
Let's focus on the overall time comparison for now: for 5 players, the difference in runtime is not large. The brute-force approach guarantees perfect results, and it only takes 42% longer than playing a White Elephant game.
But as the number of players grows, brute force takes significantly longer. Look at this silly graph:
Although you can actually zoom into these graphs (created using Plotly.js), it would probably be easier to take a look at the log-scale version, which shows the exponential (actually, factorial) growth of the brute force approach. Meanwhile, White Elephant chugs along with relatively-moderate growth.
For a 9 player game, White Elephant runs about 100 million times faster (literally: 108), and we know from the rank analysis that 99% of the resulting games are in the top 18% of possible outcomes. Not bad for the speedup! For even larger games, the trend points towards even better results.
This year at my family's Christmas party, we had a 21-player game of White Elephant. I did not run a simulation of this because I would like to use my laptop again before the heat death of the universe, but I believe the outcome was good relative to all possible outcomes.
Caveats
Obviously, these simulations are missing several important details. Here's some of the big ones I thought of:
- A 101-point scale is probably too granular - no one cares about valuing so precisely.
- This also means there might be a sample size issue for Pareto-optimality in larger games, since the (random) player preferences can make Pareto-optimality more likely - remember the 2-player example above, where all possible outcomes are Pareto-optimal.
- Similarly, uniformly random preferences seem unlikely. We've all been in games before where there are universally loved and hated gifts (thanks Johnny).
- There is no strategy around the steal limitations: a savvy player might delay stealing their favorite item unless doing so would max out the steal count - otherwise it could be stolen away again.
-
There is no representation of inter-player dynamics:
- Theft satisfaction. Last year, my friend Jackson spent a couple minutes setting up a pair of light-up fingerless gloves, and I really enjoyed stealing them afterwards (much more than if I had just revealed the gloves myself).
- Theft guilt. In the reverse direction, you might feel bad for stealing something that someone else obviously loves - even if it's your favorite among the available gifts.
- Collusion between players. Family members or partners will (if they're nice to each other) spend their own opportunities to steal gifts for their loved ones. Yee Aun and I basically merge our preferences, which changes how we see available items.
Even so, it was fun to dissect the current naive simulation.
Conclusion and next steps
White Elephant is good! Measurably so!
Over the course of this project, I spent much more time thinking about White Elephant than I thought I ever would. On the flip side, it was much easier to write the simulation and analyze the results than it is to reason abstractly about the system based on the rules.
To sidetrack a bit: White Elephant as an algorithm feels very easy to compute, as a group of real-life people ("The design is very human."). The rules and priorities are easy-enough for each person to make decisions quickly in real-time, and no one needs to know everything or make decisions based on other people's preferences. By comparison to some other algorithms, quicksort and mergesort are very inhuman sorting algorithms; people usually do something like insertion sort in real life (perhaps with a round of radix/bucket sort initially, if there are a lot of items), since the merge and partition operations are very unnatural. Does anyone know if there's a name for this concept of a human-implementable algorithm?
Back to White Elephant: this rabbit hole is very deep, and we are nowhere near the bottom. There's a lot of potential future work. Besides the caveats from above, here are a few more that come to mind:
- Simulate all potential White Elephant player orders for a given set of preferences, since it's a path-dependent game. I suspect that this could have a large impact on an individual game, but would not really affect the aggregate over different preference sets, since it's random already.
- Play with other rule variants to see how the game changes: a different number of max steals, or the variant where the first player's final steal can ignore the max steals. This could be a nice way to settle on a ruleset.
-
Compare the results of other item allocation heuristics: for example, what if all items are revealed
up-front and players just greedily pick their favorites? White Elephant might be a good approximation
compared to brute force (the most expensive possible way to do it), but the top-k graph suggests there
might be even better ways to give people what they want.
- Edit: Thanks Arun for pointing me to maximum (weighted) bipartite matching for algorithms that are likely to do better than White Elephant (in runtime, if not fun). This also brought back a suppressed memory from college: I implemented a graph algorithm for image segmentation, but finished so close to the deadline that I could only submit 2 out of 100 images (the professor gave me full credit and thought it was funny).
I also think it would also be really fun to visualize and simulate individual games in the browser, like the Raft visualization. As part of debugging, I had some logging that looked like this:
P1's turn!
1 reveals Gift A
Total score: 79 (+79)
P2's turn!
2 steals Gift A from 1 (steal count: 1)
Total score: 83 (+4)
P1's turn!
1 reveals Gift B
Total score: 115 (+32)
P3's turn!
3 steals Gift A from 2 (steal count: 2)
Total score: 115 (+0)
Imagine seeing gifts bounce between players with a live score update. Then you could change how players decide to steal, or try different rulesets, and see how it affects the resulting outcomes. Any collaborators out there?
For any future work, here is the GitHub repo, which contains the simulation code and some of the interesting analysis and visualization.
Happy holidays, and start planning your White Elephant for next year!
-Bobbie and Yee Aun
More reflection about this project on my blog: White Elephant and "fixed time, variable scope".
Special thanks to Frank Li for lots of ideas, feedback, and analysis help. Thanks Arun and Johnny for feedback. Favicon icon is Elephant by Nur Achmadi Yusuf from Noun Project (CC BY 3.0).